The angle of the flow line depends on the flow direction, which was determined in the previous step. Repeat this process for each flow line, ensuring that they are evenly spaced and cover the entire system. Figure Box 5-7 – The (b) isotropic flow net on the right is transformed back to the (a) anisotropic geometry on the left. Alternatively, we could multiply the x-coordinates of the ellipse by the ratio .
1 Flow Nets by Graphical Construction

Fayers and Sheldon (1962) were among the first to advocate steady-state numerical simulation in the study of regional hydrogeology. Remson et al. (1965) used the method to predict the effect of a proposed reservoir on groundwater levels in a sandstone aquifer. Freeze and Witherspoon (1966) generated many numerical flow nets in their theoretical study of regional groundwater flow. The method was in wide use much earlier in the agricultural drainage field (see Luthin and Gaskell, 1950) and in the derivation of seepage patterns in earth dams (Shaw and Southwell, 1941).
Step 2: Drawing the Flow Lines
Sketching a circle within the shapes can help discern whether the shapes are curvilinear squares. The misfits need to be large enough such that it is necessary to add or delete flow or equipotential lines in order to obtain the near-curvilinear squares as in the transition from the previous figure to this figure. The use of a resistance network as an electrical analog is based on the same principles as the conductive-paper analog. In this approach [Figure 5.11(c)] the flow field is replaced by a network of resistors connected to one another at the nodal points of a grid. The flow of electricity through each resistor is analogous to the flow of groundwater through a flow tube parallel to the resistor and having a cross-sectional area reflected by the resistor spacing times a unit depth. (5.20) must now be viewed as the current, and the σ is equal to 1/R, where R is the resistance of the resistor.
Heterogeneous Systems and the Tangent Law
This will help you determine the appropriate spacing for the flow lines and equipotential lines. In conclusion, analyzing the flow net is a crucial step in understanding the behavior of fluid flow within a system. It allows you to identify areas of convergence and divergence, determine the flow rate and velocity, and analyze potential problems that may arise. By carefully examining the flow pattern and interpreting the flow net, you can gain valuable insights into the hydraulic behavior of the system and make informed decisions regarding its design or operation. The spacing between equipotential lines represents the change in hydraulic head or potential energy between two points. By measuring this spacing and using the principles of fluid mechanics, you can calculate the flow velocity.
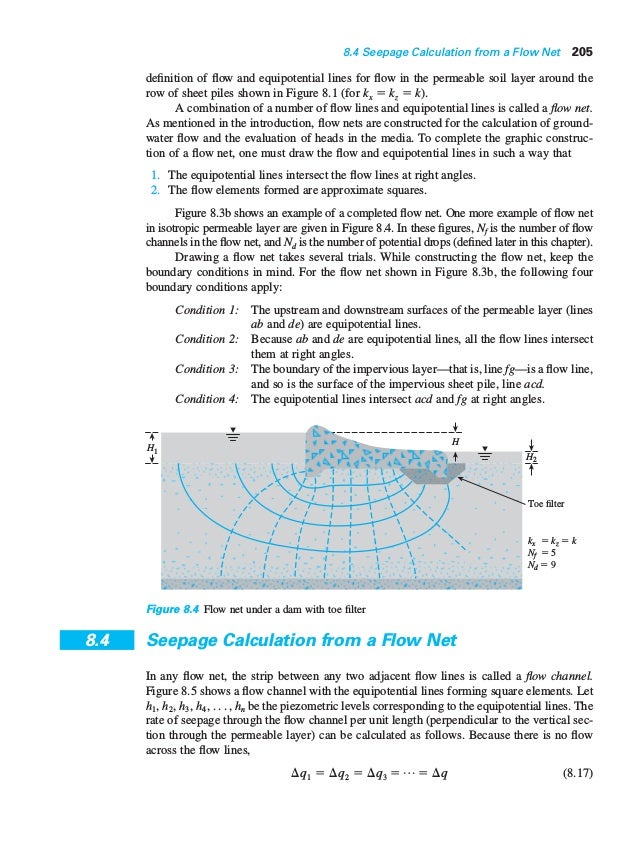
Uplift Pressure (Pu)
- Computer approaches are more versatile, but require knowledge in use of software.
- Such flexibilities mean that numerically calculated equipotential lines and flow lines do not necessarily form shapes of constant aspect ratio, and flow tubes do not necessarily carry the same volumetric flow rate.
- These curves of hydraulic conductivity, K, and moisture content, θ as a function of ψ, are the wetting curves taken from Figure 2.13.
- The construction of flow nets is one of the most powerful analytical tools for the analysis of groundwater flow.
These tools provide a grid system that allows for precise measurements and ensures that your flow lines and equipotential lines are drawn accurately. The grid system helps maintain the proper spacing and alignment of the lines, making it easier to analyze the flow pattern later on. In that case, the draw flow nets flow lines and equipotential lines of a flow net will not meet at right angles. This result was obtained after sketching and erasing until all of the criteria were met. A rough sketch of the equipotential lines provides an estimate of the number of head drops that will create curvilinear squares.
Saturated-unsaturated flow nets are required to explain perched water tables (Figures 2.15 and Figure 6.11), and to understand the hydrogeological regime on a hillslope as it pertains to streamflow generation (Section 6.5). Reisenauer (1963) and Jeppson and Nelson (1970) utilized numerical simulation to look at the saturated-unsaturated regime beneath ponds and canals. Their solutions have application to the analysis of artificial recharge of groundwater (Section 8.11). Freeze (1971b) considered the influence of the unsaturated zone on seepage through earth dams (Section 10.2). Numerical methods were introduced to the groundwater hydrology literature by Stallman (1956) in an analysis of regional water levels.
Make sure to follow the proper equations and formulas to determine the appropriate distances between the lines. Additionally, verify that the flow lines are drawn in the correct direction, as this is crucial for accurately representing the flow system. Adjust the position of flow lines and equipotential lines until a circle fills the space between the lines fairly well as in Figure 9. The number of flow lines is the same in Figure 8 and Figure 9, but the number of equipotential lines differ indicating the redrawing was necessary to obtain a flow net that can be used to calculate flow through the system.
To illustrate inclusion of a water table in a flow net, consider flow through an earthen dam with a hydraulic conductivity of 0.2 m/d resting on an impermeable base (Figure Box 4-1). The dam extends 55 m in the direction perpendicular to the diagram, and is capped with impermeable material such that water is prevented from infiltrating the surface of the dam. Water enters from the up-gradient reservoir on the left and exits to the downstream reservoir on the right. Unconfined groundwater systems have a water table boundary which requires special consideration when drawing a flow net because the location of the water table boundary is not known until an acceptable flow net has been drawn.
Figure Box 5-5 – Geometric transformation of the (a) anisotropic system on the left to an (b) isotropic system on the right by transforming the vertical axis. The transformed geometry on the right is 4 times taller and as wide as the left one. Because the same flow pattern repeats itself in alternating mirror images throughout the field, only a small portion of the drained field needs to be drawn to develop a flow net (Figure Box 5-4).
For example, the first equipotential line to the right of the upper reservoir will have a value of 24.44 m and so the intersection of the equipotential line and the water table should be at that elevation. There is another type of flow net that is extremely difficult to construct by graphical means. For flow problems that involve both saturated and unsaturated flow, 犀利士
steady-state flow nets are usually derived by numerical simulation.
If the shapes are not circular, as in the first attempt to draw a flow net shown in Figure 8, then the lines should be adjusted. However, for cases in which the hydraulic conductivity is non-homogeneous (i.e., heterogeneous), constructing a flow net requires a numerical method using a computer. Once the elevation grid is drawn, proceed to sketch the equipotential lines at right angles to no-flow boundaries and flow lines. Make sure that equipotential lines meet the water table and the seepage face at an elevation that is the same as the hydraulic head of the equipotential line. The equipotential lines and flow lines should intersect to form curvilinear squares. As before, one way to decide if you are creating curvilinear squares is to draw a circle between the intersecting lines.




